How and Why
I hadn’t planned on undertaking another weekend project. My last one was spectacularly destroyed, and another became almost immediately useless with the latest updates of ChatGPT. All things considered, I was content to spend my recent weekends (almost literally) on the couch.
However, the other day, while delving deep into Google for work research, I stumbled upon something familiar that sparked a wave of nostalgia: Conway’s Game of Life. It was casually mentioned in one of the articles I was reading, and it took me back.
A bit of context: I’ve always enjoyed tinkering with computers. Back in high school, we had a dedicated computer lab filled with rows of PCs. For someone who grew up in a seaside town, this was a real novelty. Students weren’t allowed to use the lab whenever they wanted; there were scheduled times for its use. But whenever I could, I went there. I tinkered a lot, and one of the things I created was an implementation of Conway’s Game of Life in Macromedia Flash.
I know, the name of that software alone should reveal my age.
It was a simple little thing I created; filled with too many loops and unnecessary conditionals, but it was exportable as an executable and fully functional. I enjoyed watching the patterns evolve and expand, collapse, and dissipate into nothingness. I liked testing new patterns. Whenever I felt bored, I opened it and tested new patterns. I kept it with me for a long time, I think until grade 12, when my tinkering hobby was replaced by the duty to prepare for national exams.
That’s a story for another time, by the way. National exams. So much drama.
Anyway, fast forward to the present: I read up again about Conway’s Game of Life, the rules, the algorithm, and realised that I could make this a weekend project: create an implementation of the Game of Life. And knowing that lately I’ve been working (almost) exclusively with Go, I decided to make it in Go!
Hence, over the weekend, “La Vie en Go” was born.
The Game
The Basics
If this is your first time hearing about the Game of Life, I’d suggest you read up on the Wikipedia article of Conway’s Game of Life. Nevertheless, I’ll try to summarise it as concisely and clearly as possible.
The game itself was conceived by a British mathematician named John Conway, back in 1970. It’s essentially an automaton, or a zero-player game, meaning no outside input could be made after the initial state. It could be played on an infinite or finite grid, and each grid would act as a cell.
During the game, each cells would be in one of the two possible states: dead or alive. The cells would be updated for every time unit passed, which we could call generation.
The Rules
The state of each cells across generations would be determined by four simple rules, which govern the whole game:
- Birth: A dead cell with exactly three live neighbors becomes alive.
- Survival: A live cell with two or three live neighbors stays alive.
- Death by Isolation: A live cell with fewer than two live neighbors dies.
- Death by Overcrowding: A live cell with more than three live neighbors dies.
Now that the rules are clear, we moved forward to the implementation.
The Code
The key components of the La Vie en Go could be summed up into the following:
The Cell
As explained above, in a Game of Life, each grid would constitute a cell, and it’d have two states: dead or alive. The cell alone was easy to define using struct, and the must-have properties would be the X and Y coordinates of the cell.
type Cell struct {
X, Y int
}
I was tempted to add the state of the cell as one of the properties, but decided to be against it and define it elsewhere—in my case, as mapping value. I’ll explain this part later.
Now that the cell is defined, we’d need to be able to input the initial state.
The Input Parser
I spent more time in this part than the others, to be honest. I was really thinking and asking myself: how would I or someone else want to use this program? Like, what’s the easiest ways for people to input the initial pattern’s coordinates? In the end, I decided to settle on three methods:
- using command-line flags,
- using
*stdin*, - using interactive prompt.
The next question that arise was the format of the input. I wanted something as
simple as possible, so I decided a format like "x1 y1, x2 y2, ..." would be
good. But then I wondered: the Conway’s Game of Life should be playable on
infinite grid, but for practical reason of course I couldn’t do that for a game
played on the terminal.
Thus, I decided to add two variables: MaxX and MaxY. I defined them inside
the main() because this value would be used by other functions surely:
func main() {
// Define the boundaries
MaxX, MaxY := 60, 20
}
So with the boundaries defined, and the logic for accepting inputs defined, there needs to be the function that will parse the inputs and return the desired variable.
Firstly, the inputs that would be accepted would surely be in the format of
strings. Something like "x1 y1, x2 y2" . Next, the desired output of the parse
should be the Cell and (here’s where it gets interesting) its state. To
make the computation as efficient as possible, I decided to pack all the pairs
of cell-state together, thus in the form of map, and then, I decided to make
it so that I’d only always churned the live cells only—making the rest of the
cells automatically in the state of dead.
And of course, I also need to make sure that the parsed coordinates would be
within the boundaries of MaxX and MaxY.
With all those, the parsing function thus written as follows:
func parseCoordinates(input string, MaxX, MaxY *int) map[Cell]bool {
// Prepare the mapping of live cells
liveCells := make(map[Cell]bool)
// Expect input like `x1 y1, x2 y2, x3 y3`. Thus, split first
// on comma and parse one by one afterwards.
parts := strings.Split(input, ",")
for _, part := range parts {
coords := strings.Fields(strings.TrimSpace(part))
if len(coords) != 2 {
continue
}
// Try parsing the string coordinate to integer
x, err1 := strconv.Atoi(coords[0])
y, err2 := strconv.Atoi(coords[1])
// Verify that there's no error and coordinates within boundaries
if err1 != nil || err2 != nil || x < 1 || x > *MaxX || y < 1 || y > *MaxY {
continue
}
// If all's good add the live Cell to the map
liveCells[Cell{X: x, Y: y}] = true
}
return liveCells
}
With that parsing function ready, I wrote the function that would read the initial input pattern:
func readInitialCoordinates(MaxX, MaxY *int) map[Cell]bool {
coordsFlag := flag.String(
"c", "", "Initial live cells coordinates (e.g., -c \"1 3, 3 4\")")
flag.Parse()
// Command line coordinates provided
if *coordsFlag != "" {
return parseCoordinates(*coordsFlag, MaxX, MaxY)
}
// Check if data is being piped into stdin
info, _ := os.Stdin.Stat()
if (info.Mode() & os.ModeCharDevice) == 0 {
input, err := io.ReadAll(os.Stdin)
if err != nil {
fmt.Println("Error reading input:", err)
os.Exit(1)
}
return parseCoordinates(string(input), MaxX, MaxY)
}
// Interactive mode: prompt for input
fmt.Printf(
"Enter live cell coordinates (x y), and then press Enter twice to start. Max X=%d, Max Y=%d:",
MaxX, MaxY)
scanner := bufio.NewScanner(os.Stdin)
scanner.Scan() // Read the first line of input
return parseCoordinates(scanner.Text(), MaxX, MaxY)
}
I then added the readInitialCoordinates() to the main() function, taking
the MaxX and MaxY values that are already defined there:
func main() {
// Define the boundaries
MaxX, MaxY := 60, 20
// Read the initial inputted coordinates as map of live cells
liveCells := readInitialCoordinates(&MaxX, &MaxY)
}
Now that we already have the functions to take the input for the initial state,
the next logical thing is to try to print the pattern. For this, let’s make a
simple printer function that’ll take the liveCells map, the MaxX and MaxY,
and print the live cells with symbol # while the other cells (dead state) with
symbol . :
func printBoard(liveCells map[Cell]bool, MaxX, MaxY *int) {
fmt.Print("\033[H\033[2J\033[3J") // Clear up the whole terminal first
for y := 1; y <= *MaxY; y++ {
for x := 1; x <= *MaxX; x++ {
if liveCells[Cell{X: x, Y: y}] {
fmt.Print("#")
} else {
fmt.Print(".")
}
}
// If we change y, we change line
fmt.Println()
}
}
and put them inside the main function:
func main() {
// Define the boundaries
MaxX, MaxY := 60, 20
// Read the initial inputted coordinates as map of live cells
liveCells := readInitialCoordinates(&MaxX, &MaxY)
printBoard(liveCells, &MaxX, &MaxY)
}
Now with those, if you tried to run it with the following command, for example:
go run main.go -c "13 11, 13 12, 13 13, 12 12, 14 12"
You’ll see the following output:
............................................................
............................................................
............................................................
............................................................
............................................................
............................................................
............................................................
............................................................
............................................................
............................................................
............#...............................................
...........###..............................................
............#...............................................
............................................................
............................................................
............................................................
............................................................
............................................................
............................................................
............................................................
So far, we’ve managed to take our input pattern, parse it, and display the live and dead cells. The next part is where the logic of the game would be really implemented: how to make the cells evolve over time.
The Cells Evolution
If you’ve been following the creation of this Game of Life from the start above, this should be your current code:
package main
import (
"bufio"
"flag"
"fmt"
"io"
"os"
"strconv"
"strings"
)
type Cell struct {
X, Y int
}
func parseCoordinates(input string, MaxX, MaxY *int) map[Cell]bool {
// Prepare the mapping of live cells
liveCells := make(map[Cell]bool)
// Expect input like `x1 y1, x2 y2, x3 y3`. Thus, split first
// on comma and parse one by one afterwards.
parts := strings.Split(input, ",")
for _, part := range parts {
coords := strings.Fields(strings.TrimSpace(part))
if len(coords) != 2 {
continue
}
// Try parsing the string coordinate to integer
x, err1 := strconv.Atoi(coords[0])
y, err2 := strconv.Atoi(coords[1])
// Verify that there's no error and coordinates within boundaries
if err1 != nil || err2 != nil || x < 1 || x > *MaxX || y < 1 || y > *MaxY {
continue
}
// If all's good add the live Cell to the map
liveCells[Cell{X: x, Y: y}] = true
}
return liveCells
}
func readInitialCoordinates(MaxX, MaxY *int) map[Cell]bool {
coordsFlag := flag.String(
"c", "", "Initial live cells coordinates (e.g., -c \"1 3, 3 4\")")
flag.Parse()
// Command line coordinates provided
if *coordsFlag != "" {
return parseCoordinates(*coordsFlag, MaxX, MaxY)
}
// Check if data is being piped into stdin
info, _ := os.Stdin.Stat()
if (info.Mode() & os.ModeCharDevice) == 0 {
input, err := io.ReadAll(os.Stdin)
if err != nil {
fmt.Println("Error reading input:", err)
os.Exit(1)
}
return parseCoordinates(string(input), MaxX, MaxY)
}
// Interactive mode: prompt for input
fmt.Printf(
"Enter live cell coordinates (x y), and then press Enter twice to start. Max X=%d, Max Y=%d:",
MaxX, MaxY)
scanner := bufio.NewScanner(os.Stdin)
scanner.Scan() // Read the first line of input
return parseCoordinates(scanner.Text(), MaxX, MaxY)
}
func printBoard(liveCells map[Cell]bool, MaxX, MaxY *int) {
fmt.Print("\033[H\033[2J\033[3J")
for y := 1; y <= *MaxY; y++ {
for x := 1; x <= *MaxX; x++ {
if liveCells[Cell{X: x, Y: y}] {
fmt.Print("#")
} else {
fmt.Print(".")
}
}
// If we change y, we change line
fmt.Println()
}
}
func main() {
// Define the boundaries
MaxX, MaxY := 60, 20
// Read the initial inputted coordinates as map of live cells
liveCells := readInitialCoordinates(&MaxX, &MaxY)
printBoard(liveCells, &MaxX, &MaxY)
}
The next step is to create a function that updates the cells to mirror their evolution over time, following the previously established rules.
Essentially, the state of each cell in the next generation is determined by the states of its neighbouring cells in the current generation. A cell has eight neighbours in its immediate vicinity: to the north, northeast, east, southeast, south, southwest, west, and northwest. We can represent the relative positions of these neighbours as a slice of Cell objects, as shown here:
NeighborOffsets := []Cell{
{0, 1}, // North
{1, 1}, // Northeast
{1, 0}, // East
{1, -1}, // Southeast
{0, -1}, // South
{-1, -1}, // Southwest
{-1, 0}, // West
{-1, 1}, // Northwest
}
With the neighborOffsets defined, we can step into defining what is
essentially the core function of our Game of Life, a function that I call
updateCells().
The Core of Evolution: Starting the updateCells() Function
Starting from this part, I’ll try to explain the function, and how they came to be, bit by bit, step by step.
Firstly, this function takes three parameters: liveCells, which is a map
representing the current generation’s live cells; MaxX and MaxY, which point
to the integers defining the visible boundaries of our world.
In return, it’ll return another map of live cells for the next generation, and two boolean parameters: one that’ll tell if there’s still any living cell in the visible world, and another that’ll tell if there’s still any changes in the world.
func updateCells(liveCells map[Cell]bool, MaxX, MaxY *int) (
map[Cell]bool, bool, bool,
) {
// cont.
Inside this function, we put the neighborOffsets parameter inside. This slice
will be used later on by other logic inside the function.
// cont.
NeighborOffsets := []Cell{
{0, 1}, // North
{1, 1}, // Northeast
{1, 0}, // East
{1, -1}, // Southeast
{0, -1}, // South
{-1, -1}, // Southwest
{-1, 0}, // West
{-1, 1}, // Northwest
}
// cont.
Building the Next Generation: nextGen and candidateCells
Next, we create two parameters, both being maps of Cells. The first one is
nextGen, a fresh map that’ll be used to store the coordinates of cells that’ll
become alive in the next generation, and the other one is candidateCells,
which is basically a map that is tracking potential cells that might spring to
life based on the neighbouring count of live cells.
// cont.
nextGen := make(map[Cell]bool)
candidateCells := make(map[Cell]int)
// cont.
Afterwards, come the part where we literally build the next generation. We
iterate through each live cell and we assess its immediate neighbouring
cells based on the neighborOffsets . Principally, for each live cell, we count
the number of its living neighbours. At the same time, we populate the
candidateCells map with dead cells that are adjacent to the live ones, to mark
them as the potential live cells.
// cont.
for cell := range liveCells {
neighborsCount := 0
for _, offset := range NeighborOffsets {
neighbor := Cell{X: cell.X + offset.X, Y: cell.Y + offset.Y}
if liveCells[neighbor] {
neighborsCount++
} else {
candidateCells[neighbor]++
}
}
// cont.
By applying the Game of Life rules, we decide the fate of each cell. A live cell with two or three neighbours survives; otherwise, it perishes. Similarly, a dead cell with exactly three live neighbouring cells will come alive.
// cont.
if neighborsCount == 2 || neighborsCount == 3 {
nextGen[cell] = true
}
}
// Birth the candidate cell if it has three neighbouring
// alive cells.
for cell, count := range candidateCells {
if count == 3 {
nextGen[cell] = true
}
}
// cont.
Finally, we come to the part where we’ll check if the game should continue or not.
So, basically, to ascertain the continuation of our game, we will verify two things:
- at least one cell in the
nextGenresides within the boundaries of our visible world - check if there’s any change between generations, basically checking if the world has become stagnant or not.
Once both check are done, we return the nextGen cells and the results of the
two checks above.
// cont.
// Check if any live cells are within the boundaries.
// This determines if the game should continue.
anyWithinBoundaries := false
for cell := range nextGen {
if cell.X >= 1 && cell.X <= *MaxX && cell.Y >= 1 && cell.Y <= *MaxY {
anyWithinBoundaries = true
break
}
}
// Check if the world has become stagnant between generations.
// This determines if the game should continue.
changed := !areMapsEqual(liveCells, nextGen)
return nextGen, anyWithinBoundaries, changed
}
// updateCells function's finished.
// Helper function to check if two Cell maps are equal.
func areMapsEqual(a, b map[Cell]bool) bool {
if len(a) != len(b) {
return false
}
for k := range a {
if !b[k] {
return false
}
}
return true
}
Finalising the main() Function
At this point, we already have the following updateCells() and its helper
function, areMapsEqual() :
func updateCells(liveCells map[Cell]bool, MaxX, MaxY *int) (
map[Cell]bool, bool, bool,
) {
NeighborOffsets := []Cell{
{0, 1}, // North
{1, 1}, // Northeast
{1, 0}, // East
{1, -1}, // Southeast
{0, -1}, // South
{-1, -1}, // Southwest
{-1, 0}, // West
{-1, 1}, // Northwest
}
nextGen := make(map[Cell]bool)
candidateCells := make(map[Cell]int)
for cell := range liveCells {
neighborsCount := 0
for _, offset := range NeighborOffsets {
neighbor := Cell{X: cell.X + offset.X, Y: cell.Y + offset.Y}
if liveCells[neighbor] {
neighborsCount++
} else {
candidateCells[neighbor]++
}
}
if neighborsCount == 2 || neighborsCount == 3 {
nextGen[cell] = true
}
}
for cell, count := range candidateCells {
if count == 3 {
nextGen[cell] = true
}
}
// Check if any live cells are within the boundaries.
// This determines if the game should continue.
anyWithinBoundaries := false
for cell := range nextGen {
if cell.X >= 1 && cell.X <= *MaxX && cell.Y >= 1 && cell.Y <= *MaxY {
anyWithinBoundaries = true
break
}
}
// Check if the world has become stagnant between generations.
// This determines if the game should continue.
changed := !areMapsEqual(liveCells, nextGen)
return nextGen, anyWithinBoundaries, changed
}
// Helper function to check if two Cell maps are equal.
func areMapsEqual(a, b map[Cell]bool) bool {
if len(a) != len(b) {
return false
}
for k := range a {
if !b[k] {
return false
}
}
return true
}
Now it’s time to put them to the main() function to run the Game of Life. So
far, we already have the following main function:
func main() {
// Define the boundaries
MaxX, MaxY := 60, 20
// Read the initial inputted coordinates as map of live cells
liveCells := readInitialCoordinates(&MaxX, &MaxY)
printBoard(liveCells, &MaxX, &MaxY)
}
Basically, with that alone, we have already been able to take the user input of the initial live cells within the visible universe. Next, we should iterate through generations to run the game, generating new live or dead cells. Because we want the game to keep running until a conditional break happens, we start by putting those parameters in order and initialising the infinite loop:
func main() {
MaxX, MaxY := 60, 20
liveCells := readInitialCoordinates(&MaxX, &MaxY)
var changed, anyWithinBoundaries bool
for {
printBoard(liveCells, &MaxX, &MaxY)
// cont.
As you can see we moved the printBoard() function within the loop now, so the
first iteration is already within the virtual ticking clock of the world. We
also created two variables: one to check the changing of the world and the other
to check if there’s any living cells within the boundaries.
Next, we run the updateCells() :
// cont.
liveCells, anyWithinBoundaries, changed = updateCells(liveCells, &MaxX, &MaxY)
// cont.
at this stage, we actually already have the decision on whether or not the game would continue. But for visibility, we shall pause the game shortly so that the changes in the world could be observed by the user:
// cont.
time.Sleep(250 * time.Millisecond)
// cont.
Then we move to the termination conditions. We basically just check if either
the anyWithinBoundaries or changed variables have been turned to false.
If any of them are so, we simply print the last generation, print the
end-of-the-world status, and break the infinity loop:
if !changed || !anyWithinBoundaries {
printBoard(liveCells, &MaxX, &MaxY)
if !changed {
fmt.Println("No more changes, stopping the game.")
} else {
fmt.Println("No more live cells within the boundaries, stopping the game.")
}
break
}
And so the main() function becomes:
func main() {
MaxX, MaxY := 60, 20
liveCells := readInitialCoordinates(&MaxX, &MaxY)
var changed, anyWithinBoundaries bool
for {
printBoard(liveCells, &MaxX, &MaxY)
liveCells, anyWithinBoundaries, changed = updateCells(liveCells, &MaxX, &MaxY)
// Pause the time a bit for visibility
time.Sleep(250 * time.Millisecond)
// If there are no more changes or no live cells within the boundaries, stop the game.
if !changed || !anyWithinBoundaries {
printBoard(liveCells, &MaxX, &MaxY)
if !changed {
fmt.Println("No more changes, stopping the game.")
} else {
fmt.Println("No more live cells within the boundaries, stopping the game.")
}
break
}
}
}
The Conclusion
At this end, you’d have the following code inside the main.go :
package main
import (
"bufio"
"flag"
"fmt"
"io"
"os"
"strconv"
"strings"
"time"
)
type Cell struct {
X, Y int
}
func parseCoordinates(input string, MaxX, MaxY *int) map[Cell]bool {
// Prepare the mapping of live cells
liveCells := make(map[Cell]bool)
// Expect input like `x1 y1, x2 y2, x3 y3`. Thus, split first
// on comma and parse one by one afterwards.
parts := strings.Split(input, ",")
for _, part := range parts {
coords := strings.Fields(strings.TrimSpace(part))
if len(coords) != 2 {
continue
}
// Try parsing the string coordinate to integer
x, err1 := strconv.Atoi(coords[0])
y, err2 := strconv.Atoi(coords[1])
// Verify that there's no error and coordinates within boundaries
if err1 != nil || err2 != nil || x < 1 || x > *MaxX || y < 1 || y > *MaxY {
continue
}
// If all's good add the live Cell to the map
liveCells[Cell{X: x, Y: y}] = true
}
return liveCells
}
func readInitialCoordinates(MaxX, MaxY *int) map[Cell]bool {
coordsFlag := flag.String(
"c", "", "Initial live cells coordinates (e.g., -c \"1 3, 3 4\")")
flag.Parse()
// Command line coordinates provided
if *coordsFlag != "" {
return parseCoordinates(*coordsFlag, MaxX, MaxY)
}
// Check if data is being piped into stdin
info, _ := os.Stdin.Stat()
if (info.Mode() & os.ModeCharDevice) == 0 {
input, err := io.ReadAll(os.Stdin)
if err != nil {
fmt.Println("Error reading input:", err)
os.Exit(1)
}
return parseCoordinates(string(input), MaxX, MaxY)
}
// Interactive mode: prompt for input
fmt.Printf(
"Enter live cell coordinates (x y), and then press Enter twice to start. Max X=%d, Max Y=%d:",
MaxX, MaxY)
scanner := bufio.NewScanner(os.Stdin)
scanner.Scan() // Read the first line of input
return parseCoordinates(scanner.Text(), MaxX, MaxY)
}
func printBoard(liveCells map[Cell]bool, MaxX, MaxY *int) {
fmt.Print("\033[H\033[2J\033[3J")
for y := 1; y <= *MaxY; y++ {
for x := 1; x <= *MaxX; x++ {
if liveCells[Cell{X: x, Y: y}] {
fmt.Print("#")
} else {
fmt.Print(".")
}
}
// If we change y, we change line
fmt.Println()
}
}
func updateCells(liveCells map[Cell]bool, MaxX, MaxY *int) (
map[Cell]bool, bool, bool,
) {
NeighborOffsets := []Cell{
{0, 1}, // North
{1, 1}, // Northeast
{1, 0}, // East
{1, -1}, // Southeast
{0, -1}, // South
{-1, -1}, // Southwest
{-1, 0}, // West
{-1, 1}, // Northwest
}
nextGen := make(map[Cell]bool)
candidateCells := make(map[Cell]int)
for cell := range liveCells {
neighborsCount := 0
for _, offset := range NeighborOffsets {
neighbor := Cell{X: cell.X + offset.X, Y: cell.Y + offset.Y}
if liveCells[neighbor] {
neighborsCount++
} else {
candidateCells[neighbor]++
}
}
if neighborsCount == 2 || neighborsCount == 3 {
nextGen[cell] = true
}
}
for cell, count := range candidateCells {
if count == 3 {
nextGen[cell] = true
}
}
// Check if any live cells are within the boundaries.
// This determines if the game should continue.
anyWithinBoundaries := false
for cell := range nextGen {
if cell.X >= 1 && cell.X <= *MaxX && cell.Y >= 1 && cell.Y <= *MaxY {
anyWithinBoundaries = true
break
}
}
// Check if the world has become stagnant between generations.
// This determines if the game should continue.
changed := !areMapsEqual(liveCells, nextGen)
return nextGen, anyWithinBoundaries, changed
}
// Helper function to check if two Cell maps are equal.
func areMapsEqual(a, b map[Cell]bool) bool {
if len(a) != len(b) {
return false
}
for k := range a {
if !b[k] {
return false
}
}
return true
}
func main() {
MaxX, MaxY := 60, 20
liveCells := readInitialCoordinates(&MaxX, &MaxY)
var changed, anyWithinBoundaries bool
for {
printBoard(liveCells, &MaxX, &MaxY)
liveCells, anyWithinBoundaries, changed = updateCells(liveCells, &MaxX, &MaxY)
// Pause the time a bit for visibility
time.Sleep(250 * time.Millisecond)
// If there are no more changes or no live cells within the boundaries, stop the game.
if !changed || !anyWithinBoundaries {
printBoard(liveCells, &MaxX, &MaxY)
if !changed {
fmt.Println("No more changes, stopping the game.")
} else {
fmt.Println("No more live cells within the boundaries, stopping the game.")
}
break
}
}
}
If you try running it with the same command as the example above:
go run main.go -c "13 11, 13 12, 13 13, 12 12, 14 12"
You’d get the following:
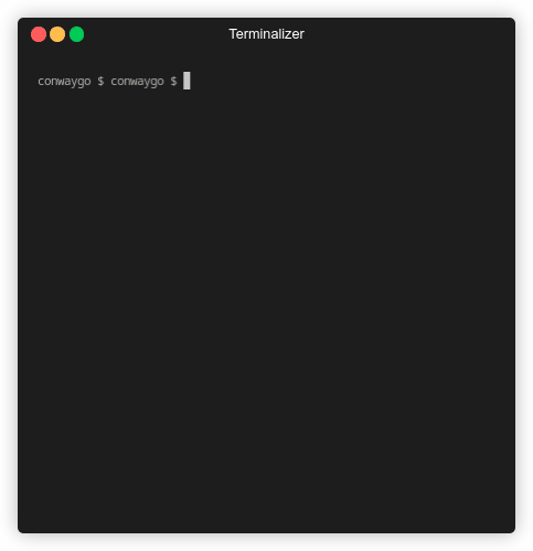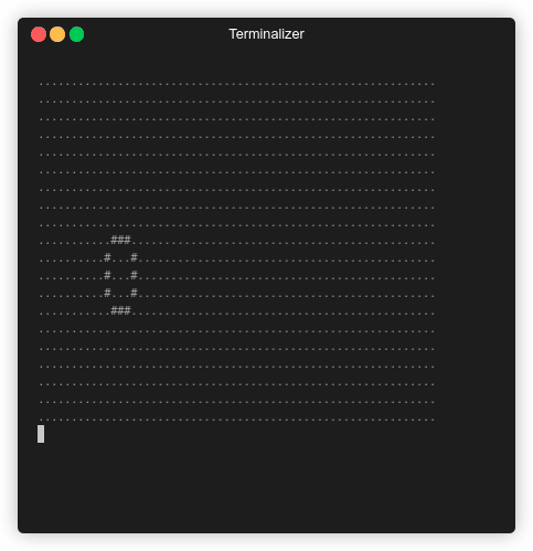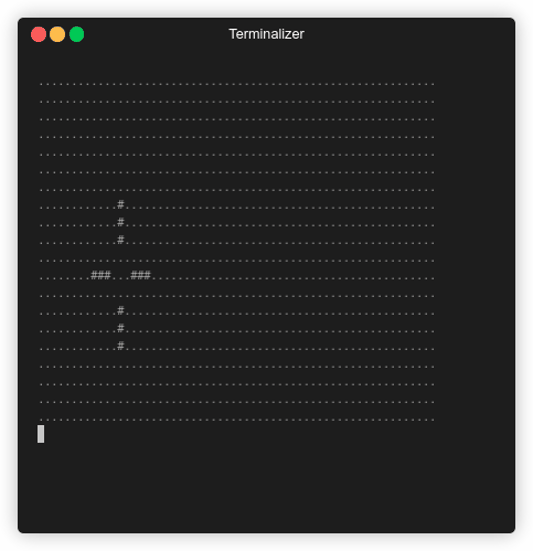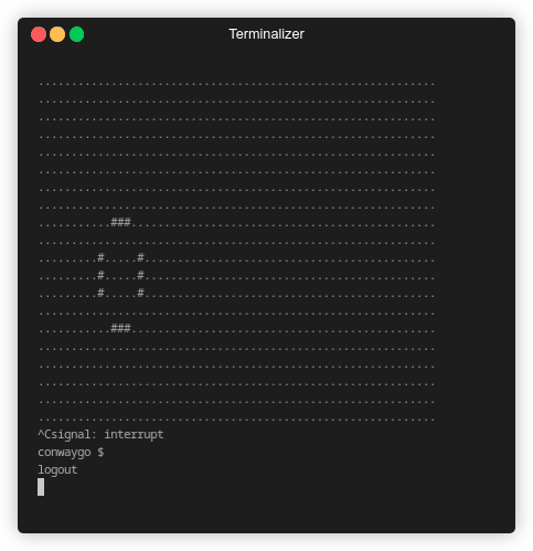
As we can see our initial cells evolve to form a type of blinker, which is a pattern that’ll endlessly repeating.
Some pattern will disappear after a while. For example, the following pattern that resembled a heart:
go run main.go -c "14 7, 15 7, 16 7, 20 7, 21 7, 22 7,
13 8, 17 8, 19 8, 23 8,
12 9, 24 9,
11 10, 25 10,
11 11, 25 11,
12 12, 24 12,
13 13, 23 13,
14 14, 15 15, 16 16, 17 17, 19 17, 20 16, 21 15, 22 14"
will result as follows:
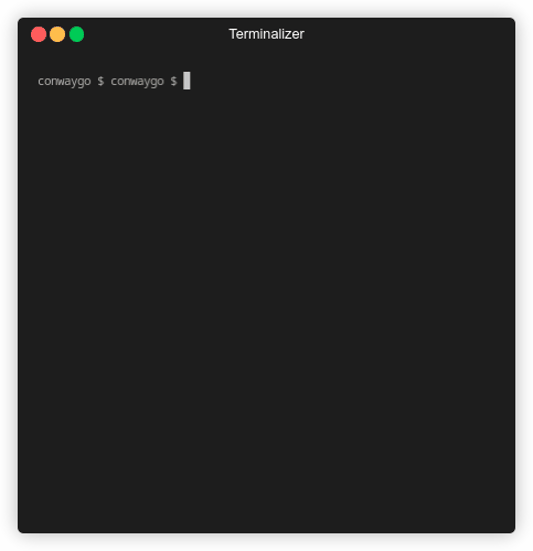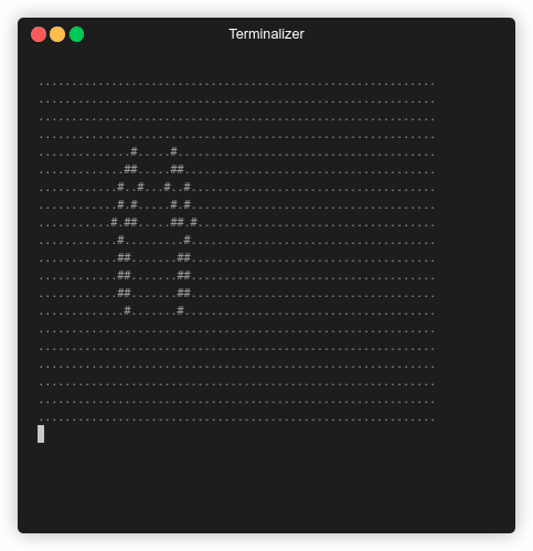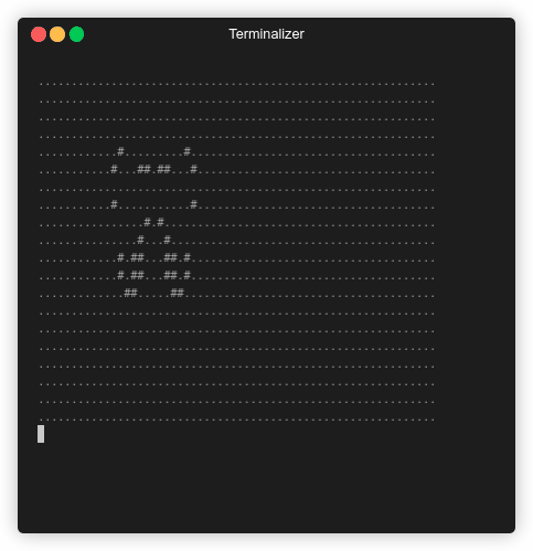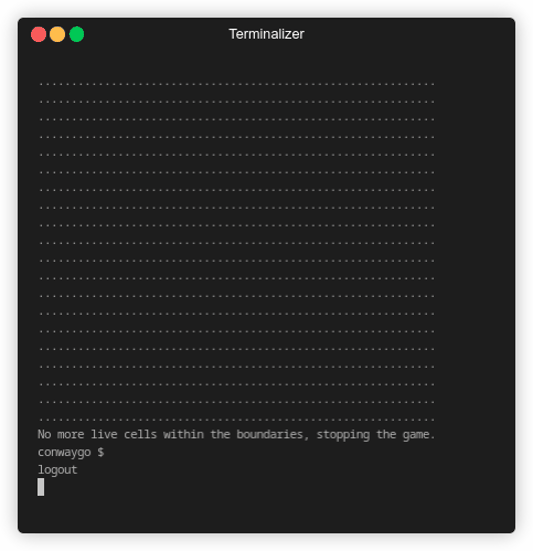
As we can see, because there’s no more alive cells within the visible world within the boundaries, the game stopped.
There are so many patterns to be explored; I encourage you to try!
The Epilogue
I started this whole weekend project out of nostalgia and to be honest it’s kinda worth it. I don’t know what it is about this game but for me, working on my computer while having a little terminal open, displaying blinker or various pattern emerges and re-emerges over time on this game is kind of… therapeutic and somehow improve my focus. I don’t know why.
On the other hand, watching the game running with various patterns, I was reminded of how so many intricate behaviours can sprout from a handful of basic rules and initial state. I think the Game of Life is a vast ocean full of possibility. This game, with its initial state and simple rules defining the entirety of its world, is looking like an intriguing reflection of our own universe. It’s a nice that reminder that our beginnings and the rules we adhere to can shape our existence, mirroring our reality.
Probably hence the name, the Game of Life.
Anyway that’s it for this weekend’s coding project! If you have any questions, if you found any bugs, or have any feature requests, feel free to submit them as Issues in the GitHub repository.